Building Higher Education Comparison Groups: A Data Science Informed Approach
Distance measures are an important component of many techniques found used throughout data science. Distance measures are any measure that can help us quantify the distance between two points in any given coordinate system. This Tech Tip is based on a related article, Applied Distance Measures; Building Higher Education Comparison Groups. Below is a summary of what distance measures are and how they can be used in the process of building comparison groups. Further, below is a list of helpful references you may review for additional guidance on this topic.
What Are Distance Measures?
Imagine for a moment a traditional scatter plot, including an x-axis and a y-axis forming a coordinate system. Further imagine, as shown in Figure 1, that we placed along one axis an institution’s enrollment and, along the other axis, that institution’s tuition costs. This setup would allow us to plot various institutions based on these two institutional characteristics. As shown in the figure below, there are four hypothetical institutions (A through D).
Figure 1
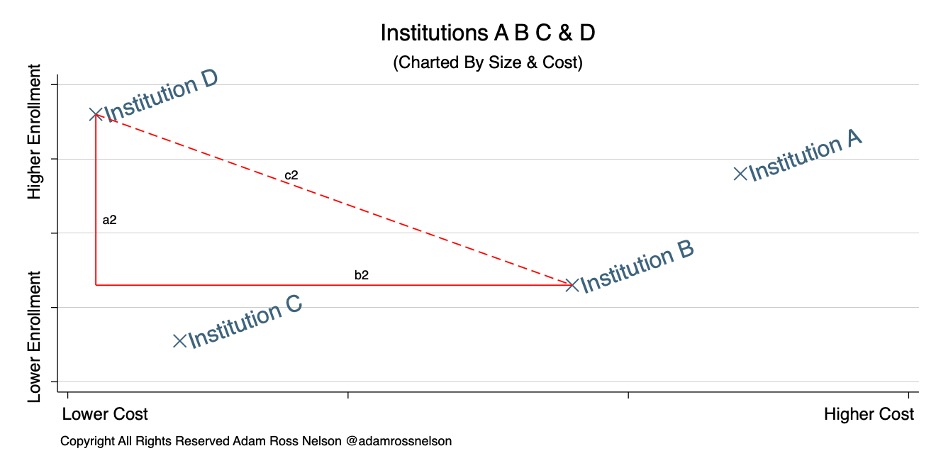
Distance measures let us find the distance between any two points within the coordinate system. For example, as shown in the figure, the dashed line labeled c2 would graphically represent the distance between Institution B and Institution D. A relatively simple application of the Pythagorean theorem (a2 + b2 = c2) reveals the distance between Institution B and Institution D.
The distance measure can also serve as a measure of similarity. The closer items are in the given coordinate system, the more alike they are. In the figure above, for example, it might be useful to know which institution is most similar to Institution D. A visual review of the figure produces ambiguous results. However, an empirical review, using distance measures, reveals that Institution C is closest to Institution D. Thus, Institution C is more similar to Institution D than either Institutions B or A.
Distance in Three (or More) Dimensions
Finding distance measures in a three (-plus) dimensional space is nearly identical to the process of finding distance in a two-dimensional space. The video from this IPEDS Educator Web Conference, IPEDS Meets Data Science: New-ish Methods For Peer Groupings , and accompanying slide presentation, offer a detailed walk-through on the process of finding distance in higher-dimensional spaces.
The video also introduces other distance measure methods other than Pythagorean’s. The remainder of this article offers guidance on how institutional researchers may apply these distance measures in the work of building institutional comparison groups.
Building Comparison Groups
Imagine that an institution receives criticism in the form of negative print, online, and social media attention focused on the institution’s undergraduate application fee rates. Many institutions might respond to this negative attention with an analysis of application fees among similar institutions. Institutions could use these distance measures to identify meaningful comparison groups.
Why Not Use Existing Comparison Groups?
A variety of sources, including the U.S. Department of Education (U.S. DOE), have established comparison groups among higher education institutions. For example, the U.S. DOE’s National Center for Education Statistics (NCES) specifies approximately 240-260 comparison groups for its "Data Feedback Reports.”
According to NCES, “the NCES automation comparison group for degree-granting institutions is based on control type, Carnegie Classification, and enrollment size." It might be important to find comparison groups based on institutional characteristics beyond those. Calculating distance measures lets institutional researchers build comparison groups in a rigorous manner grounded in an empirical approach.
Once You Have Comparison Groups
An assist from the hypothetical institution The University of Wiscesota demonstrates how distance measures can help build comparison groups. Figure 2 shows ten institutions, including The University of Wiscesota. Based on institution state, longitude, latitude, residence hall room capacity, residence hall room charges, campus dining charges, the acceptance rate, and the yield rate, calculating distance measures resulted in the list of comparison group institutions shown in Figure 2.
Figure 2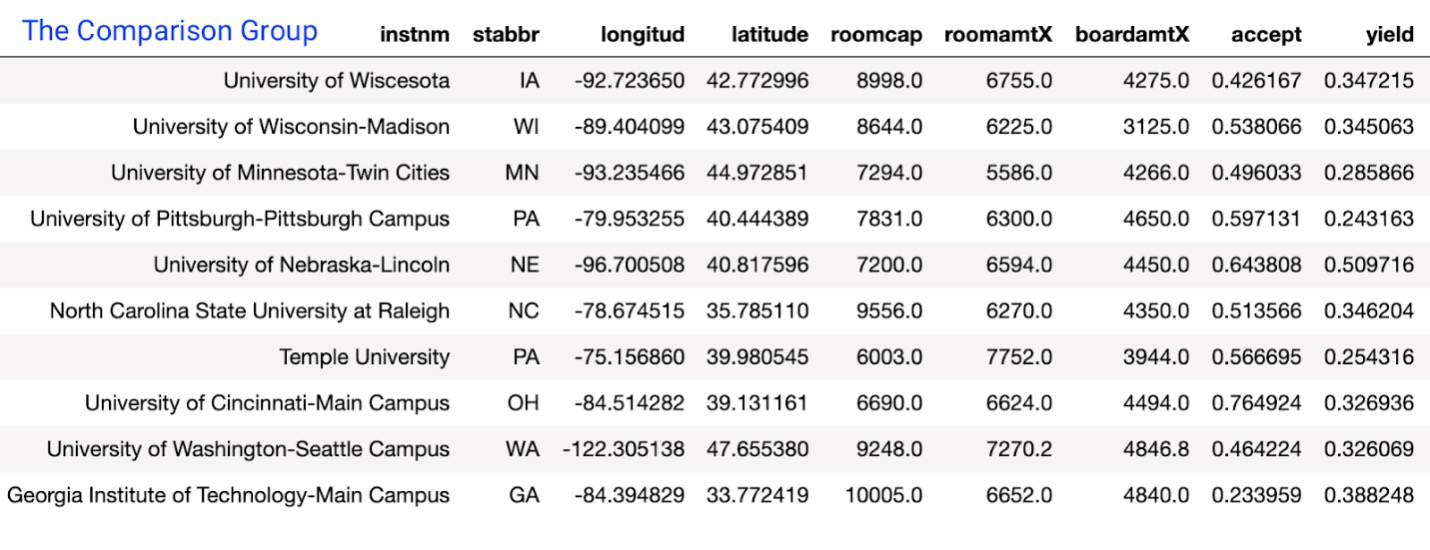
Now that we have found the comparison group, we can compare the variable of interest: undergraduate application fee amounts. Figure 3 shows undergraduate application fee amounts.
Figure 3
From this comparison, it seems that The University of Wiscesota not only asks for the lowest fee, but that the next lowest fee of $45 is more than double Wiscesota’s fee. The highest fee is nearly four times Wiscesota’s fee.
Other Uses for Distance Measures
If you have data that are observations of individuals (individual students), this technique could also work to find similar individuals. For example, continuing with the undergraduate admission’s theme, consider a scenario at Wiscesota where the dean of admissions wanted to look for a new way to identify students that are likely to perform well at the institution.
Imagine taking a list of students who completed the first year at Wiscesota and then sorting that list by first-year grade point averages to find the top ten students. The dean of admissions could then use distance measures to identify students in the subsequent year’s applicant pool that are similar to those top performing students.
Conclusion
This article summarized what distance measures are and how they can be useful to institutional research professionals in the process of building comparison groups. Further below is a list of additional references and ideas related to other comparison groups institutions might find useful.
At a base level, this article proposes the opportunity to bring novel methods to the work of institutional research. There are two articles that might be useful when looking to import the use of distance measures into practice among institutional research professionals: A Cookbook: Using Distance To Measure Similarity and Applied Distance Measures; Building Higher Education Comparison Groups.
 Adam Ross Nelson
Adam Ross Nelson
Since 2020, Adam is a consultant who provides research, data science, machine learning, and data governance services. Previously, he was the inaugural data scientist at The Common Application which provides undergraduate college application platforms for institutions around the world. He holds a PhD from The University of Wisconsin - Madison in Educational Leadership & Policy Analysis. Adam is also formerly an attorney with a history of working in higher education, teaching all ages, and working as an educational administrator. Adam sees it as important for him to focus time, energy, and attention on projects that may promote access, equity, and integrity in education. This means he strives to find ways for his work to challenge system oppression, injustice, and inequity. He is passionate about connecting with other data professionals in person and online. For more information and background look for his insights by connecting with Adam on LinkedIn, Medium, and his website at coaching.adamrossnelson.com.
